A force d’ignorer les sources traditionnelles simples et véritables de la franc-maçonnerie, surtout au cours du XIXème siècle et plus encore pendant le siècle suivant, les francs-maçons ont tenté, péniblement, de repeupler un univers symbolique désenchanté et surtout incompris à l’aide de « mystères de substitution » qui vont chercher dans les pyramides d’Égypte chères à l'inoubliable Georges Barbarin (Le secret de la Grande Pyramide, 1936), les secrets des Druides ou ceux des Druzes (!), les clés qui permettront d’éclairer à nouveau la franc-maçonnerie.
Ces excursions dans des contrées bien éloignées du lieu de naissance de la franc-maçonnerie ont souvent conduit à de pures élucubrations – et la veine est loin d’en être épuisée ! Mais aussi, une réelle méconnaissance de certains aspects de l’histoire intellectuelle de l’Europe a conduit à prêter aux bâtisseurs du Moyen Age des « secrets de l’art »qui, en réalité, se réduisent à peu de chose et, me semble-t-il, font surtout perdre beaucoup de temps en sollicitant l’attention de certains francs-maçons sur de purs mirages.
Le Nombre d’or en est un exemple flagrant…
1. Des mesures incertaines. Observons qu’en l’occurrence il s’agirait moins d’un secret – puisque tout le monde pouvait théoriquement le retrouver dans les façades des bâtiments gothiques sur lesquelles on l’avait en quelque sorte inscrit – que d’une science qui traduirait les hautes connaissances des ouvriers médiévaux ou de leurs architectes. On comprendrait des lors parfaitement que ces humbles artisans aient pu être les pères spirituels, et les maîtres sans doute, des maçons spéculatifs, malheureusement moins savants qu’eux. En d’autres termes, les commentaires et les spéculations relatives au Nombre d’or permettraient d’accréditer l’idée que les maçons opératifs étaient secrètement – comme toujours – versés dans les plus hautes mathématiques et non point seulement des ouvriers illettrés.
Tout un chacun a déjà lu ou parcouru ces ouvrages interminables ou, avec force plans sur lesquels s’étalent et se croisent les traces les plus complexes, l’on retrouve la « clé harmonique » de la façade de Reims, de Notre-Dame de Paris ou de la cathédrale de Chartres. Or, tout cela laisse immanquablement un sentiment d’artifice et de jeu vain. Reconnaissons en premier lieu, avec P. du Colombier que « les mensurations des monuments souffrent dans leur interprétation une grande part d’arbitraire et on a l’impression que, pour les faire cadrer avec telle ou telle théorie, certains auteurs, inconsciemment [?], arrangent la réalité.» [1]
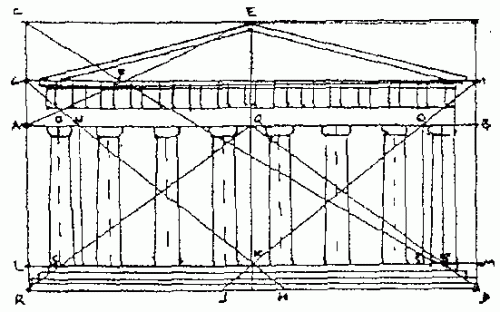
Avec un simple crayon : prouver tout... et son contraire !
C’est malheureusement une pure évidence et l’on songe, dans la même veine, a l’abondante littérature qui, dans les dimensions et les angles de la Grande Pyramide de Khéops, peut retrouver à la fois le diamètre polaire de la Terre et toutes les grandes dates de l’histoire de l’Humanité, sans compter mille autres merveilles [2]…
S’agissant des constructeurs du Moyen Age, ces laborieuses théories se heurtent en fait à deux obstacles de poids :
- Le premier est qu’en effet, sur un même plan architectural, on peut sans difficulté appliquer quatre canevas « harmoniques » fondés sur des principes entièrement différents : c’est juste une question de patience et l’effet parait tout aussi convaincant. Du reste, cela a été réalisé et démontre que l’on peut précisément tout démontrer – et son contraire [3] ! On peut alors poser une simple question : raisonnablement, à quoi tout cela mène-t-il ?
- Mais plus fondamentalement, et c’est le second point, il faut se reporter à l’état réel des connaissances mathématiques à cette époque. Comme le rappelle J. Gimpel [4], la correspondance échangée entre deux écolâtres – donc deux savants – vers 1025, montre qu’au XIème siècle l’essentiel des documents grecs sur le savoir mathématique avait bel et bien été perdu, et ce dès le haut Moyen Age. De l’analyse de ces lettres, le grand historien des sciences Paul Tannery, dans ses Mémoires scientifiques (Tome V, 1922) conclut qu’elle se réduit à des constats d’ignorance. Il faudra attendre les traductions de l’arabe aux XIIème et XIIIème siècles pour que ce savoir soit progressivement retrouvé.
2. Naissance du Nombre d’or. En ce qui concerne le célèbre Nombre d’or, la question est encore plus intéressante. A ceux qui le désignent comme la norme mathématique de la plupart des monuments de l’histoire, on peut opposer les mêmes objections que celles qui ont été mentionnées plus haut : l’arbitraire des mesures, l’approximation des relevés sur des plans qui ne reproduisent pas nécessairement les dimensions exactes de bâtiments endommagés ou érodés par le temps, ou encore le fait qu’en variant d’un écart infime l’emplacement de deux tracés, le quotient ou la « raison » qu’on leur applique peut être modifiée d’une manière bien plus considérable.
L’un des propagateurs de ces méthodes, une personnalité haute en couleur sur qui je reviendrai dans un instant, Matila Ghyka, conseillait du reste aux amateurs de ne pas se décourager si leurs premiers calculs se révélaient infructueux, et leur proposait d’essayer tous les tracés possibles jusqu’à trouver celui qui s’accorderait avec sa théorie ! Dans de telles conditions, en effet, le succès est assuré…
Mais il y a davantage à en dire. L’affaire du Nombre d’or est très révélatrice des circonstances dans lesquelles s’élabore une légende « ésotérique » [5].
C’est Euclide qui, dans ses Éléments, le grand traite de mathématiques de l’Antiquité [6], au Livre XIII, décrit sans y attacher particulièrement la « division en moyenne et extrême raison » qui peut notamment générer le pentagone mais permet également d’inscrire dans un cercle des corps réguliers, comme l’icosaèdre (20 triangles équilatéraux) et surtout le dodécaèdre (12 pentagones). Après lui, aucun commentaire particulier n’est connu sur cette proportion jusqu’au tout début du XVIème siècle, quand un mathématicien franciscain, Luca Pacioli, publie un traité intitule De divina proportione. [7]
Luca Pacioli (c. 1445-1517)
Théologien au moins autant que savant, il ne peut résister à l’envie de rapprocher les mathématiques de la science sacrée : comme on compte treize effets de la division en moyenne et extrême raison, il les rapporte « aux douze Apôtres auquel s’ajoute notre Sauveur » et voit dans le dodécaèdre, qui pour Platon symbolisait l’univers, l’évocation de Dieu : voilà pourquoi la proportion est divine !
Mais Pacioli ne va plus loin, ne donne à cette proportion aucune vertu esthétique et ne parle pas du « Nombre d’or » – personne, à son époque, n’en a d'ailleurs encore parlé.
Il faudra attendre le début du XIXème siècle pour que des mathématiciens allemands s’emparent de ce thème et, le tout premier, Adolf Zeising [8], auteur en 1854 d’un ouvrage intitule Neue Lehre von de Proportionen des menschlichen Körpers (Nouvelles leçons sur les proportions du corps humain), va faire un sort a cette proportion désormais qualifiée par lui de « section d’or », où il voit un critère de beauté universelle et singulièrement la norme des proportions du corps humain. Parmi ses émules, il faut surtout citer Franz Liharzik, un homme curieux qui se prétendait possesseur de mille sortes de sciences [9] et pour qui, en1865 dans son livre Das Quadrat, la section d’or est « la loi morphologique fondamentale qui imprègne toute la nature et qui doit constituer le fondement de la structure de l’univers » : cette conviction n’engageait que lui et n’eut alors que peu d’écho.
3. La thèse de Matila Ghyka. Mais on doit surtout à Matila Ghyka [10], évoqué plus
haut, d’avoir véritablement « inventé » le Nombre d’or auquel il donnera une signification tout à fait nouvelle. Dans deux ouvrages publiés entre 1927 et 1931 [11], il annonce que le Nombre d’or – car c’est ainsi qu’on le nommera désormais, d’après lui – résume la tradition pythagoricienne tout entière, laquelle aurait régi les monuments antiques et toutes les cathédrales gothiques, et aurait été transmise depuis cette époque, d’âge en âge, par une chaine d’initiés : confréries de bâtisseurs, Steinmetzen, guildes anglaises, Compagnons français, sans oublier cela va sans dire, les alchimistes et les Rose-Croix…
Ghyka, à l’érudition touffue, confuse et incertaine, ne dit jamais d’où il tire de si extraordinaires révélations, ni sur quoi il fonde ses affirmations. Il assène avec une certitude tranquille et nombre d’esprits légers ou exaltés, depuis lors, n’ont cessé de le plagier. Il reste qu’on chercherait vainement, avant lui, la moindre trace d’un document susceptible de corroborer ces théories plutôt extravagantes dont aucune source pythagoricienne antique ne fait état et, bien entendu, ni dans les Carnets de Villard de Honnecourt, ni dans les « divulgations » de Roriczer [12] ne figure jamais cette « divine proportion » comme règle d’un « tracé harmonique » !
"Le" livre fondateur...
Bref, on l’aura compris : le Nombre d’or n’a fait son entrée dans la tradition maçonnique et n’est connu des francs-maçons que depuis que certains d’entre eux, au cours des décennies récentes, ont rapporté, souvent sans en soupçonner l’origine, les rêveries échevelées de Matila Ghyka [13]…
Résumons-nous : de même qu’il ne faut pas accorder aux architectes du Moyen Age une science géométrique qu’ils ne possédaient pas encore, en dépit de leur réel talent pratique, de même il ne faut pas leur attribuer la science de subtilités mathématiques dont rien n’atteste en leur temps et qui ne furent explicitées que bien plus tard.
Après tout, l’émotion esthétique que suscitent les grandes églises médiévales, le sens artistique qu’elles révèlent chez ceux qui les conçurent, la foi profonde et l’audace technique dont elles témoignent, sont leurs plus beaux titres de gloire. Les créditer de secrets sans fondement et sans substance n’y ajoute vraiment rien et ne fait même que brouiller leur image en travestissant la vérité.
* Cette note est inspirée d'un passage de mon livre L’invention de la franc-maçonnerie, Paris, Véga, 2009, 2011.
[1] 1. P. du Colombier, Les chantiers des cathédrales, Paris, 1953, p. 92.
[2] Voici une soixantaine d’années déjà, dans un livre a la fois drôle et dévastateur, le grand archéologue et architecte J.-P. Lauer a montre l’inanité de toutes ces pseudo-démonstrations : Le problème des pyramides d’Égypte, Paris, 1948.
[3] F. Benoit, L’architecture, l’Occident médiéval, 2 vol., Paris, 1933, II, 303.
[4] J. Gimpel, Les bâtisseurs des cathédrales, Paris, 1958, p. 117.
[5] Sur cette question, il faut de reporter au livre implacable et superbement documenté de M. Neveux, Le nombre d’or, radiographie d’un mythe, Paris, 1995.
[6] Les 13 livres de Eléments, écrits vers 300 avant notre ère et constamment transmis depuis lors, furent imprimes des 1482 a Venise.
[7] Venise, 1509. Le titre complet de l’ouvrage est d’ailleurs très évocateur des intentions de son auteur : œuvre nécessaire à tous les esprits perspicaces et curieux, où chacun de ceux qui aiment étudier la philosophie, la perspective, la peinture, la sculpture, l’architecture, la musique et les autres disciplines mathématiques, trouvera une très délicate, subtile et admirable doctrine et se délectera de diverses questions touchant une très secrète science.
[8] (1810-1876) Philosophe et professeur a Leipzig puis a Munich.
[9] (1813-1866) Docteur en médecine, il se disait a la fois chirurgien, pédiatre, ophtalmologue, accoucheur, et avait sillonne toutes les villes d’Europe centrale.
[10] Ne en 1881 en Roumanie d’une famille qui avait servi le Tsar de Russie – Ghyka avait droit au titre de Prince –, il sera élevé a Paris. Polyglotte, il fera l’École navale, l’École supérieure d’électricité et obtiendra aussi un doctorat en droit. Diplomate roumain, il fut en poste dans diverses capitales européennes. Ruine en 1946, il émigra aux USA où il devint professeur d’esthétique et d’histoire de l’art. Il mourut en Virginie en 1965.
[11] L’Esthétique des proportions dans la nature et dans les arts, Paris, 1927 et Le Nombre d’or. Rites et rythmes pythagoriciens dans le développement de la civilisation occidentale, 2 vol., Paris, 1931
[12] Un certain Mathias Roriczer, Parlier de son père Conrad, avait rejoint en 1473 la Fraternite des Steinmetzen. Il suivit son père dans sa carrière, notamment en tant que maitre maçon à la cathédrale de Ratisbonne. Entre 1486 et 1490, en violation des règles imposées, il publia trois opuscules « pour le bien du public » (c’est-à-dire de tous ceux qui n’appartenaient pas au métier !) dans lesquelles il exposait notamment la méthode permettant d’élever un pinacle à partir de diagrammes en deux dimensions (Büchlein von der Fialen Gerechtigkeit) : très exactement ce qu interdisaient les Statuts de 1459...
[13] Sur les plus extrêmes réserves qu’on doit formuler à leur propos – et à propos de tous les ajouts de la même veine qui sont apparus dans le sillage de Matila Ghyka – voir notamment: http://www.pseudo-sciences.org/spip.php?article796(Le mythe du nombre d'or)